WGS84坐标系理解

核心概念

关系图

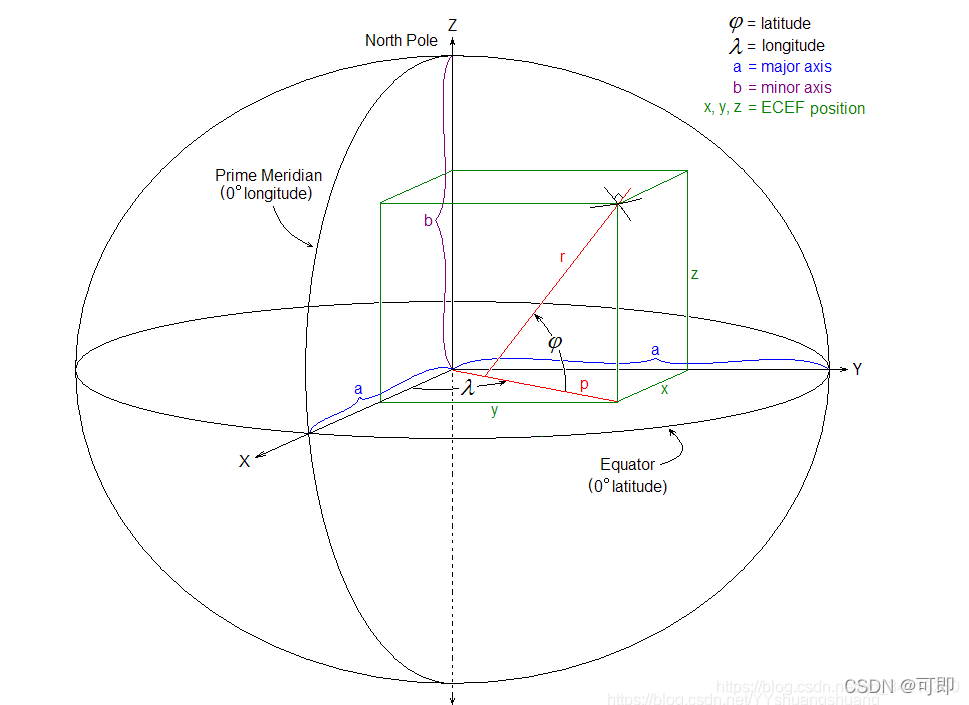
定义

ecef的z轴指向北极,x轴是本初子午线和赤道的交汇处,由地心指向,y轴则是满足右手坐标系

wgs84定义在椭球面上,LLA(对应x轴方向夹角经度lon,z方向夹角维度lat,和相对于椭球面高度alt)

enu是一个局部坐标系,我们计算体积盒AABB的时候,通过ENU坐标系计算

### 注意

wgs84坐标系非笛卡尔坐标系,1° 经度的实际距离 ≈ 111km × cos(φ),切记不要用wgs84直接计算AABB包围盒

转化方法

ENU <-> ECEF

def ecef_to_enu(lat1, lon1, alt1, lat0, lon0, alt0):
    """
    ECEF → ENU

    Args:
        x, y, z: 目标点的ECEF坐标（米）
        lat0, lon0, alt0: 参考点的LLA坐标（度，度，米）

    Returns:
        (e, n, u): ENU坐标（米）
    """
    # Step 1: 计算参考点的ECEF坐标
    x, y, z = geodetic_to_ecef(lat1, lon1, alt1)
    x0, y0, z0 = geodetic_to_ecef(lat0, lon0, alt0)

    # Step 2: 计算相对向量（平移）
    dx = x - x0
    dy = y - y0
    dz = z - z0

    # Step 3: 转弧度
    lat0_rad = np.radians(lat0)
    lon0_rad = np.radians(lon0)

    # Step 4: 构造旋转矩阵
    sin_lat = np.sin(lat0_rad)
    cos_lat = np.cos(lat0_rad)
    sin_lon = np.sin(lon0_rad)
    cos_lon = np.cos(lon0_rad)

    # 旋转矩阵（3x3）
    R = np.array(
        [
            [-sin_lon, cos_lon, 0],
            [-sin_lat * cos_lon, -sin_lat * sin_lon, cos_lat],
            [cos_lat * cos_lon, cos_lat * sin_lon, sin_lat],
        ]
    )

    # Step 5: 应用旋转
    enu = R @ np.array([dx, dy, dz])

    return enu[0], enu[1], enu[2]

ENU=R⋅XYZ (绕x轴旋转经度和绕y轴旋转90-纬度)的欧拉角公式

enu->ecef 是 R^-1

ECEF<->LLA

参考文档

def xyz2llh(x, y, z):
    """
    Function to convert xyz ECEF to llh
    convert cartesian coordinate into geographic coordinate
    ellipsoid definition: WGS84
      a= 6,378,137m
      f= 1/298.257

    Input
      x: coordinate X meters
      y: coordinate y meters
      z: coordinate z meters
    Output
      lat: latitude rad
      lon: longitude rad
      h: height meters
    """
    # --- WGS84 constants
    a = 6378137.0
    f = 1.0 / 298.257223563
    # --- derived constants
    b = a - f * a
    e = math.sqrt(math.pow(a, 2.0) - math.pow(b, 2.0)) / a
    clambda = math.atan2(y, x)
    p = math.sqrt(pow(x, 2.0) + pow(y, 2))
    h_old = 0.0
    # first guess with h=0 meters
    theta = math.atan2(z, p * (1.0 - math.pow(e, 2.0)))
    cs = math.cos(theta)
    sn = math.sin(theta)
    N = math.pow(a, 2.0) / math.sqrt(math.pow(a * cs, 2.0) + math.pow(b * sn, 2.0))
    h = p / cs - N
    while abs(h - h_old) > 1.0e-6:
        h_old = h
        theta = math.atan2(z, p * (1.0 - math.pow(e, 2.0) * N / (N + h)))
        cs = math.cos(theta)
        sn = math.sin(theta)
        N = math.pow(a, 2.0) / math.sqrt(math.pow(a * cs, 2.0) + math.pow(b * sn, 2.0))
        h = p / cs - N
    llh = {"lon": clambda, "lat": theta, "height": h}
    return llh

实际生产过程中还是推荐用 pyproj

    from pyproj import Transformer, CRS
    
    transformer_inv = Transformer.from_crs("EPSG:4978", "EPSG:4326", always_xy=True)
    lon2, lat2, alt2 = transformer_inv.transform(x, y, z)
    print(f"LLA Coordinates: lon={lon2}, lat={lat2}, alt={alt2}")

ENU/ECEF/WGS84坐标系理解#

核心概念#

定义#

### 注意#

转化方法#

ENU <-> ECEF#

ECEF<->LLA#